Day 3 - Factoring Polynomials

Complex Numbers

The complex numbers encompass both real numbers and imaginary numbers, forming a broad category of numbers useful in algebra and beyond.

The set of complex numbers is denoted by \(\mathbb{C}\) and can be written in the form: \[ z = a + bi \] where:

• \(a\) is the real part of the complex number.
• \(bi\) is the imaginary part, with \(b\) being a real number and \(i\) being the imaginary unit, where \(i^2 = -1\).

---

Real Numbers

The real numbers (\(\mathbb{R}\)) are numbers that can be found on the number line and are divided into several subsets:

1. Rational Numbers (\(\mathbb{Q}\)): Numbers that can be expressed as a fraction \(\frac{p}{q}\), where \(p\) and \(q\) are integers, and \(q \neq 0\). Subsets of rational numbers include:

• Integers (\(\mathbb{Z}\)):
  Whole numbers and their negatives:
  \[ \mathbb{Z} = \{\dots, -3, -2, -1, 0, 1, 2, 3, \dots\} \]

• Whole Numbers (\(\mathbb{W}\)):
  Non-negative integers, starting from \(0\):
  \[ \mathbb{W} = \{0, 1, 2, 3, \dots\} \]

• Natural Numbers (\(\mathbb{N}\)):
  Positive counting numbers:
  \[ \mathbb{N} = \{1, 2, 3, \dots\} \]

2. Irrational Numbers: Numbers that cannot be expressed as a fraction, with non-repeating, non-terminating decimals. Examples: \(\sqrt{2}, \pi, e\).

---

Imaginary Numbers

An imaginary number involves the square root of a negative number. The simplest imaginary number is \(i\), where:

\[ i = \sqrt{-1} \quad \text{and} \quad i^2 = -1 \]

Examples:

• \(\sqrt{-4} = 2i\)
• \(i^3 = i \cdot i^2 = i \cdot (-1) = -i\)
• \(i^4 = (i^2)^2 = (-1)^2 = 1\)

Imaginary numbers are not on the real number line but are represented on a different axis (the imaginary axis) in the complex plane.

---

The Complex Plane

The complex plane is a two-dimensional coordinate system where:

• The horizontal axis represents the real part of a complex number.
• The vertical axis represents the imaginary part.

A complex number \(z = a + bi\) can be represented as a point \((a,b)\) or a vector in the complex plane.

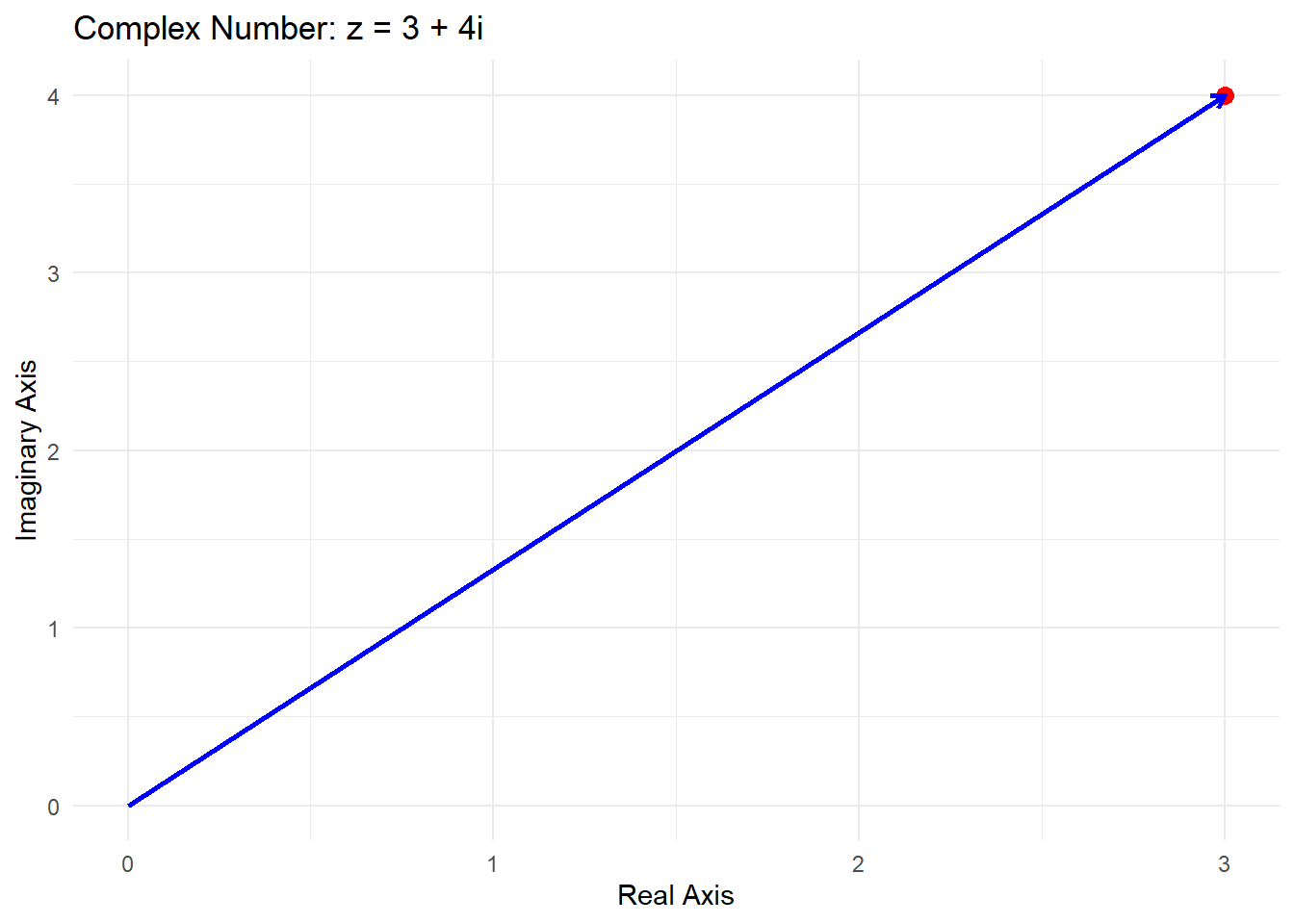
Example: The complex number \(z = 3 + 4i\) is plotted as the point \((3,4)\) where: - \(a = 3\) (real part) - \(b = 4\) (imaginary part)

---

Operations with Complex Numbers

Addition and Subtraction

To add or subtract two complex numbers, combine the real parts and imaginary parts separately:

\[(a + bi) + (c + di) = (a + c) + (b + d)i\] Example:

\[ (3 + 5i) + (1 - 3i) = (3 + 1) + (5 - 3)i = 4 - 2i\] ## Multiplication

To multiply two complex numbers, use the distributive property and \(i^2 = -1\):

\[(a + bi)(c + di) = ac + adi + bci + bdi^2 = (ac - bd) + (ad + bc)i\]

Example:

\[ (3 + 5i)(1 - 3i) = 3 - 9i + 5i - 15i^2 = 18 - 4i\]

Division

To divide one complex number by another, multiply both the numerator and denominator by the conjugate of the denominator:

\[ \frac{a + bi}{c + di} = \frac{a + bi}{c + di} \cdot \frac{c - di}{c - di} = \frac{(a + bi)(c - di)}{(c + di)(c - di)} \]

Recall that:

\[ (c + di)(c - di) = c^2 - d^2i^2 = c^2 + d^2 \]

So the division becomes:

\[ \frac{(a + bi)(c - di)}{c^2 + d^2} = \frac{(ac + bd) + (bc - ad)i}{c^2 + d^2} \]

Example:

\[ \frac{3 + 5i}{1 - 3i} \cdot \frac{1 + 3i}{1 + 3i} = \frac{(3 + 5i)(1 + 3i)}{(1 - 3i)(1 + 3i)} \]

The denominator simplifies as:

\[ (1 - 3i)(1 + 3i) = 1^2 + 3^2 = 1 + 9 = 10 \]

Now, simplify the numerator:

\[ (3 + 5i)(1 + 3i) = 3(1) + 3(3i) + 5i(1) + 5i(3i) = 3 + 9i + 5i + 15i^2 = 3 + 14i - 15 = -12 + 14i \]

Thus, the division is:

\[ \frac{3 + 5i}{1 - 3i} = \frac{-12 + 14i}{10} = -1.2 + 1.4i \]

Comparison

Complex numbers cannot be compared using standard inequalities (e.g., \(<\), \(>\)) since they have both real and imaginary parts. However, we can compare their magnitudes.

The magnitude (or modulus) of a complex number \(a + bi\) is defined as:

\[ |a + bi| = \sqrt{a^2 + b^2} \]

This gives the distance from the origin in the complex plane. For example, for the complex number \(3 + 4i\), the magnitude is:

\[ |3 + 4i| = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]

Similarly, for any two complex numbers \(z_1 = a + bi\) and \(z_2 = c + di\), you can compare their magnitudes:

\[ |z_1| = \sqrt{a^2 + b^2}, \quad |z_2| = \sqrt{c^2 + d^2} \]

If \(|z_1| > |z_2|\), then \(z_1\) has a greater magnitude than \(z_2\), and vice versa.

---

Thank you for visiting! Explore the other pages for more insights and resources.